Published on February 5, 2017
Some say that building a small language interpreter, especially if a LISP, is one of those things you have to do at least one time in your life as a programmer, an eye opening experience that will give you new insights into how the tools you use everyday work and demystify a few concepts that seem daunting when seen from afar.
In this article, we’ll implement a minimal LISP based on the 1978 paper by John McCarthy titled A Micro-Manual For Lisp - Not The Whole Thruth, that defines a small and self-contained LISP, as a Swift framework that will be able to evaluate strings containing LISP symbolic expressions.
We’ll eventually use that compact interpreter to build a simple REPL (Read-Eval-Print Loop) that will interactively execute statements and print out the result of the evaluation. A playground to play around with the interpreter is also available.
This article will try to explain everything you need to known to roll out you own LISP interpreter, if you need a great weekend project. Feel free to follow along or just read the introduction, write your own and use this post as an example of an alternative implementation.
The diagram below shows the overall design of what we are going to build:
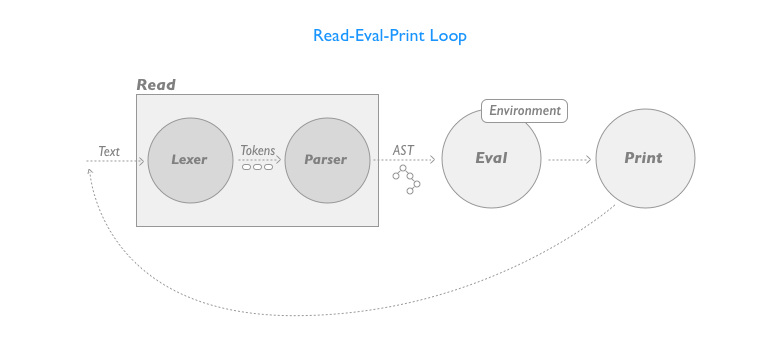
The first functional block, the Read phase, reads some text containing code and with a two-phase process produces an syntax tree with an internal representation of the input program.
The first phase, represented by the Lexer separates the input text in tokens (the building blocks, from a textual point of view, of the program) and then the Parser takes this series of tokens and produces an Abstract Syntax Tree (AST), a hierarchical representation of the source code.
Once we have an AST we’ll be able to evaluate the expression to produce a result that we’ll then print on screen for the user.
The library with the interpreter described in this article and a playground to test it are avaliable on GitHub.
Contents:
LISP Basics
Let’s start with a brief recap of what we are going to implement, looking into the McCarthy’s article that essentially contains the definition of the language.
First of all, if you are not familiar with LISP, the acronym derives from LISt Processor and that’s a good way do describe languages of the LISP family. Their essential data structure is the list and your programs will perform operations on those lists.
As you have guessed since I used the term family a lot of variants or dialects of the original LISP defined by John McCarthy exist nowadays, from traditional languages like Racket to languages like Clojure that are built on top of different technologies (the Java virtual machine and the Java runtime in this case) and are able to extend the underlying platform with the functionalities that a LISP can provide through its different paradigm.
What we are going to implement here is a minimal LISP that contains the bare essential elements to do something useful.
A LISP interpreter can be described as an evaluator of programs expressed using a peculiar recursive data structure called symbolic expression or form, something that can assume the appearance of either an Atom or a List. Atoms are simple series of alphanumeric characters that can assume different meaning whereas Lists (also called compound forms) are sequences of other symbolic expressions, represented as a sequence of values enclosed inside parenthesis.
An additional kind of form exists in this LISP, the special form that differs from other kind of symbolic expressions because has different evaluation rules for its sub-expressions.
To represent the data that your program will manipulate, we will again use the same symbolic expression data type, ending up using the same data structure to represent both you source code and the data it uses.
But what about the AST? A syntactically valid program is structured as a series of symbolic expression, in other words a series of nested lists, so when converting the source code to an AST we will again use a data structure able to store lists to model our program.
Languages like LISP, where programs and their internal representation can be expressed with the language fundamental data type are called homoiconic and this property makes meta-programming, the ability that a program has to modify itself or other programs in the same language, easier than what it is in classic non-homoiconic languages(most of those you know, Swift included). You will be able to leverage the fact that code and data share the same representation to modify your code at runtime without using complex mechanisms.
If you look at the end of the McCarthy’s paper you’ll notice that also building a LISP interpreter in LISP, called a Meta Circular Evaluator, will just be a matter of a few lines of code. The Swift interpreter we are about to build will do the same thing, it will evaluate these symbolic expressions recursively and will produce another symbolic expression as result.
But let’s see an example of a LISP program expressed using symbolic expressions:
(COUNT (QUOTE (A B C) ) 42)In the example above, COUNT, QUOTE, A, B, C, 42 are all atoms (let’s ignore their meaning for now), and each sequence between parenthesis is a list. Note how a list can contain any kind of symbolic expression, even sub-lists.
How will our interpreter evaluate this expression?
This expression will be evaluated as an expression that uses polish notation, where each list will be considered as an operator followed by the operands it needs to be applied on, e.g. a sum between two integers would be represented as (+ 1 2).
In the example above, the operator/function COUNT will be applied on the operands/parameters (QUOTE (A B C)) and 42.
And you have certainly noticed that in this definition of our language, atoms are not typed, we have a single type of atom and common types like integers, booleans and strings are not available. This LISP does not have the complex type system we find in languages like Swift.
The micro-manual defines a series of atoms that perform basic operations and describes the value they produce once a list that contains them is evaluated. In the table below, e will denote generic symbolic expressions whereas l will be used for lists.
| Atom | Structure | Description |
|---|---|---|
| Quote | (quote e1) | This atom once evaluated returns its sub expression as is, e.g. (quote A) = A |
| Car | (car l) | Returns the first element of a non-empty sub-list, e.g. (car (quote (A B C))) = A |
| Cdr | (cdr l) | Returns all the elements of the sub-list after the first in a new list, e.g. (cdr (quote (A B C))) = (B C) |
| Cons | (cons e l) | Returns a new list with e as first element and then the content of the sublist e.g. (cons (quote A) (quote (B C))) = (A B C) |
| Equal | (equal e1 e2) | Returns an atom aptly named true if the two symbolic expressions are recursively equal and the empty list () (that serves as both nil and false value) if they are not, e.g. (equal (car (quote (A B))) = (quote A)) |
| Atom | (atom e) | Returns true if the symbolic expression is an atom or an empty list if it is a lis, e.g. (atom A) = true |
| Cond | (cond (p1 e1) (p2 e2) … (pn en)) | Returns the first e expression whose p predicate expression is not equal to the empty list. This is basically a conditional atom with a slightly more convoluted syntax than a common if construct. e.g. (cond ((atom (quote A)) (quote B)) ((quote true) (quote C) = B |
| List | (list e1 e2 … en) | Returns a list of all the given expressions, identical to applying cons recursively to a sequence of expressions. |
The description contains the set of rules that will be used to evaluate these expressions.
If you look closely you’ll notice that cond is slightly different from the others since it conditionally evaluates its body depending on the sublists it contains. This is our first example of special form, we’ll pay special attention to this detail when implementing the evaluator.
Now let’s see another category of these operators, the one that is able to define functions:
| Atom | Structure | Description |
|---|---|---|
| Lambda | ( (lambda (v1 … vn) e) p1 … pn) | Defines a lambda expression with body e that describes an anonymous function that uses a series of environment variables v. This function will be evaluated using the provided parameters as value for the variables. e.g. ((lambda (X Y) (cons (car x) y) (quote (A B)) (cdr (quote (C D)))) = (A D) |
| Defun | (defun | Define a lambda expression and registers it in the current context to be used when we need it. We’ll be able to define a function like (defun cadr (X) (car (cdr x))) and use it in another expression like (cadr (quote (A B C D))). |
McCarthy’s paper describe an additional operator that can be used to define local labeled lambda expressions but we are not going to implement it, when we’ll need something similar we’ll use defun instead.
Building The Interpreter
Now that we are done describing the content of the paper it’s time to discuss the implementation of the interpreter.
In this section, each functional module that composes the interpreter will be analyzed in detail, for the full code of the interpreter check out this repository on Github.
The first aspect that need to be addressed is how symbolic expressions will be represented inside the interpreter defining how the AST will be structured. This is an important aspect since a good structure simplifies the evaluation.
Modeling Symbolic Expressions
The most obvious way to model the symbolic expressions is to use a recursive enum:
public enum SExpr{
case Atom(String)
case List([SExpr])
}Usually you need indirect when declaring a recursive enum, but in this case the array is acting as a container, so we can do without it. Other than this, there is not much to see here, this enum simply mimics the definition of symbolic expression.
Now let’s add a few other things to this enum, we’ll need a way to understand if two expressions are similar and a way to print them. For that we are going to implement Equatable and CustomStringConvertible declaring two extensions.
extension SExpr : Equatable {
public static func ==(lhs: SExpr, rhs: SExpr) -> Bool{
switch(lhs,rhs){
case let (.Atom(l),.Atom(r)):
return l==r
case let (.List(l),.List(r)):
guard l.count == r.count else {return false}
for (idx,el) in l.enumerated() {
if el != r[idx] {
return false
}
}
return true
default:
return false
}
}
}
extension SExpr : CustomStringConvertible{
public var description: String {
switch self{
case let .Atom(value):
return "\(value) "
case let .List(subxexprs):
var res = "("
for expr in subxexprs{
res += "\(expr) "
}
res += ")"
return res
}
}
}
Both functions recursively traverse the symbolic expression structure, triggering a call to themselves (using the equality operator or converting a SExpr to String), to perform their duty.
Now that the data structure has been defined let’s look into how each single component of the REPL diagram can be implemented.

Lexer and Parser
The Read phase that translates the source code to an AST to be evaluated can be divided in two stages, each one performed by a dedicated component: the Lexer and the Parser.
The main job of the Lexer or tokenizer is to perform lexical analysis on an input block of text containing the source code.
The lexer is able to break down a series of characters to a series of lexemes or tokens that represent strings that have meaning when considered in the context of a language. Tokens can be language keywords like if, operators like = or various identifiers (e.g. variable names) and literals.
Since the lexical grammar of our language, the definition of what a valid token is, is extremely simple, the lexer/tokenizer will also be simple. The Lexer will just identify string tokens separated by spaces or parenthesis.
Let’s add a read() method to SExpr to convert Strings to our enum representation and let’s start looking at the tokenize stage of the process.
extension SExpr {
/**
Read a LISP string and convert it to a hierarchical S-Expression
*/
public static func read(_ sexpr:String) -> SExpr{
enum Token{
case pOpen,pClose,textBlock(String)
}
/**
Break down a string to a series of tokens
- Parameter sexpr: Stringified S-Expression
- Returns: Series of tokens
*/
func tokenize(_ sexpr:String) -> [Token] {
var res = [Token]()
var tmpText = ""
for c in sexpr.characters {
switch c {
case "(":
if tmpText != "" {
res.append(.textBlock(tmpText))
tmpText = ""
}
res.append(.pOpen)
case ")":
if tmpText != "" {
res.append(.textBlock(tmpText))
tmpText = ""
}
res.append(.pClose)
case " ":
if tmpText != "" {
res.append(.textBlock(tmpText))
tmpText = ""
}
default:
tmpText.append(c)
}
}
return res
}
// Parser
// ...
// Read: tokenize -> parse -> result
let tokens = tokenize(sexpr)
let res = parse(tokens)
return res.subexpr ?? .List([])
}
}
The tokenize method will go through all the characters of the input string turning an opaque (from the point of view of syntax) string to a series of values defined in the Token enum. The possible values will be: pOpen (for open parenthesis), pClose (for close parenthesis) and textBlock (for every other string, representing an atom). Everything quite straightforward, since there are no special rules that could make the content read invalid.
Let’s talk about the Parser now.
The purpose of the parser is to convert a series of token into an AST the represent our code in a form easy to check for syntax errors and easy to evaluate (or optimize and compile if we are building a compiler instead of an interpreter).
We are going to implement a very simple Top-down parser that will consume the token array in its natural order and build the AST. If you plan to build a parser for a language with a more complex grammar you’d likely need something slightly more sophisticate like a Recursive Descent Parser (easy to hand code) or a LL Parser.
But for languages with complex grammar the parser is usually generated with a parser generator (e.g. ANTLR, that recently introduced support for Swift), so you’ll have to describe your grammar in a DSL instead of coding manually the parser.
The parser will be definitely more convoluted than the lexer, but again, thanks to how simple this language is, it will be a really small and simple parser.
extension SExpr {
/**
Read a LISP string and convert it to a hierarchical S-Expression
*/
public static func read(_ sexpr:String) -> SExpr{
// Tokenizer
// ...
func appendTo(list: SExpr?, node:SExpr) -> SExpr {
var list = list
if list != nil, case var .List(elements) = list! {
elements.append(node)
list = .List(elements)
}else{
list = node
}
return list!
}
/**
Parses a series of tokens to obtain a hierachical S-Expression
- Parameter tokens: Tokens to parse
- Parameter node: Parent S-Expression if available
- Returns: Tuple with remaning tokens and resulting S-Expression
*/
func parse(_ tokens: [Token], node: SExpr? = nil) -> (remaining:[Token], subexpr:SExpr?) {
var tokens = tokens
var node = node
var i = 0
repeat {
let t = tokens[i]
switch t {
case .pOpen:
//new sexpr
let (tr,n) = parse( Array(tokens[(i+1)..<tokens.count]), node: .List([]))
assert(n != nil) //Cannot be nil
(tokens, i) = (tr, 0)
node = appendTo(list: node, node: n!)
if tokens.count != 0 {
continue
}else{
break
}
case .pClose:
//close sexpr
return (Array(tokens[(i+1)..<tokens.count]), node)
case let .textBlock(value):
node = appendTo(list: node, node: .Atom(value))
}
i += 1
}while(tokens.count > 0)
return ([],node)
}
let tokens = tokenize(sexpr)
let res = parse(tokens)
return res.subexpr ?? .List([])
}
}The parse(tokens:node:) goes through every token produced by the lexer using .pOpen and .pClose to delimit lists and converts test tokens to atoms.
Notice that the parsing is performed recursively, with every nested call receiving the array of tokens left to parse and the parent list that will contain the values parsed during the next recursion step (starting with nil because the root could be an atom). When a close parenthesis is found, the list is considered complete and is returned to the caller along with the remaining tokens that still have to be parsed.
After these functions you can see the body of the read() method that execute every step in sequence returning the top-level form or an empty list (that doubles as false as we saw in the previous section) on error.
let tokens = tokenize(sexpr)
let res = parse(tokens)
return res.subexpr ?? .List([])
}
}Now that we have a working read module, let’s add something to the SExpr enum that will allow us to obtain an expression directly from a string literal without invoking manually the read() method by implementing the ExpressibleByStringLiteral protocol:
extension SExpr : ExpressibleByStringLiteral,
ExpressibleByUnicodeScalarLiteral,
ExpressibleByExtendedGraphemeClusterLiteral {
public init(stringLiteral value: String){
self = SExpr.read(value)
}
public init(extendedGraphemeClusterLiteral value: String){
self.init(stringLiteral: value)
}
public init(unicodeScalarLiteral value: String){
self.init(stringLiteral: value)
}
}With this we’ll be able to read programs directly from a string:
let expr: SExpr = "(cond ((atom (quote A)) (quote B)) ((quote true) (quote C)))"
print(expr)
print(expr.eval()!) //B
Evaluation and Default Global Environment
The evaluation phase will be more complex than what we’ve seen until now, the eval() function will recursively evaluate the AST and return the resulting evaluated symbolic expression.
First of all let’s collect all the basic operators defined by our language in a private dictionary called defaultEnvironment that will associate to every operator atom name a function of type (SExpr, [SExpr]?, [SExpr]?)->SExpr that implements it.
These function will take a SExpr parameter containing the original list (function name and parameters), evaluate it and return a SExpr as result. Those two optional arrays as second and third parameter will contain a list of variables with their values, and will be used for user-defined functions defined via defun and lamdba, in all the other cases they will just be nil. But we’ll come back to this when we’ll take a look at those operators.
To keep track of the basic builtin operators the enum Builtin has been declared with a function that keeps track of operators that don’t need sub-expression evaluation. Those are operators like quote (that exists to disable sub-expressions evaluation), special forms like cond or the lambda defining operators that will handle internally the evaluation of the sub expressions.
/// Basic builtins
fileprivate enum Builtins:String{
case quote,car,cdr,cons,equal,atom,cond,lambda,defun,list,
println,eval
/**
True if the given parameter stop evaluation of sub-expressions.
Sub expressions will be evaluated lazily by the operator.
- Parameter atom: Stringified atom
- Returns: True if the atom is the quote operator
*/
public static func mustSkip(_ atom: String) -> Bool {
return (atom == Builtins.quote.rawValue) ||
(atom == Builtins.cond.rawValue) ||
(atom == Builtins.defun.rawValue) ||
(atom == Builtins.lambda.rawValue)
}
}All the defaultEnvironment functions start with a simple check to verify that the minimum number of parameters has been provided and then proceed in building up the result to return.
Let’s take a look to a few of those, check the full project for the complete list.
/// Global default builtin functions environment
///
/// Contains definitions for: quote,car,cdr,cons,equal,atom,cond,lambda,label,defun.
private var defaultEnvironment: [String: (SExpr, [SExpr]?, [SExpr]?)->SExpr] = {
var env = [String: (SExpr, [SExpr]?, [SExpr]?)->SExpr]()
env[Builtins.quote.rawValue] = { params,locals,values in
guard case let .List(parameters) = params, parameters.count == 2 else {return .List([])}
return parameters[1]
}
env[Builtins.cdr.rawValue] = { params,locals,values in
guard case let .List(parameters) = params, parameters.count == 2 else {return .List([])}
guard case let .List(elements) = parameters[1], elements.count > 1 else {return .List([])}
return .List(Array(elements.dropFirst(1)))
}
env[Builtins.equal.rawValue] = {params,locals,values in
guard case let .List(elements) = params, elements.count == 3 else {return .List([])}
var me = env[Builtins.equal.rawValue]!
switch (elements[1].eval(with: locals,for: values)!,elements[2].eval(with: locals,for: values)!) {
case (.Atom(let elLeft),.Atom(let elRight)):
return elLeft == elRight ? .Atom("true") : .List([])
case (.List(let elLeft),.List(let elRight)):
guard elLeft.count == elRight.count else {return .List([])}
for (idx,el) in elLeft.enumerated() {
let testeq:[SExpr] = [.Atom("Equal"),el,elRight[idx]]
if me(.List(testeq),locals,values) != SExpr.Atom("true") {
return .List([])
}
}
return .Atom("true")
default:
return .List([])
}
}
env[Builtins.atom.rawValue] = { params,locals,values in
guard case let .List(parameters) = params, parameters.count == 2 else {return .List([])}
switch parameters[1].eval(with: locals,for: values)! {
case .Atom:
return .Atom("true")
default:
return .List([])
}
}
// ...
return env
}()While functions like quote or cdr just manipulate the parameter list to build an output list, the other functions like equal implement more complex logic (in this case performing a recursive equality check). To keep the source readable for didactic purposes, error checks have been kept to a minimum, additional parameters are ignored and when something goes wrong the empty list is returned.
For special forms like the conditional cond a different handling of the evaluation is required.
Conditional operators are essential to implement recursion, because only with this kind of statements we are able to decide if we can stop the recursion of proceed with another iteration.
env[Builtins.cond.rawValue] = { params,locals,values in
guard case let .List(parameters) = params, parameters.count > 1 else {return .List([])}
for el in parameters.dropFirst(1) {
guard case let .List(c) = el, c.count == 2 else {return .List([])}
if c[0].eval(with: locals,for: values) != .List([]) {
let res = c[1].eval(with: locals,for: values)
return res!
}
}
return .List([])
}The implementation of cond once it has dropped the first element of the list containing the cond atom, iterates through the list until it finds a sublist where the first member is a form with a value different from the empty list, and when it finds it, evaluates the second member of the sublist. With this kind of evaluation we evaluate only what we actually need and in case of a recursive function we don’t follow the infinite series of nested recursive calls that the body of those functions contain.
Among those functions, the defun and lambda operators are more interesting than the rest because they allow the creation of user-defined functions that are registered in a globally accessible dictionary called localContext:
/// Local environment for locally defined functions
public var localContext = [String: (SExpr, [SExpr]?, [SExpr]?)->SExpr]()Let’s see how defun (lambda is mostly identical) can be implemented.
env[Builtins.defun.rawValue] = { params,locals,values in
guard case let .List(parameters) = params, parameters.count == 4 else {return .List([])}
guard case let .Atom(lname) = parameters[1] else {return .List([])}
guard case let .List(vars) = parameters[2] else {return .List([])}
let lambda = parameters[3]
let f: (SExpr, [SExpr]?, [SExpr]?)->SExpr = { params,locals,values in
guard case var .List(p) = params else {return .List([])}
p = Array(p.dropFirst(1))
// Replace parameters in the lambda with values
if let result = lambda.eval(with:vars, for:p){
return result
}else{
return .List([])
}
}
localContext[lname] = f
return .List([])
}This function will require a list with four symbolic expressions, one for the operator name, one for the name (this as expected will be a simple atom) and the last two for the variables list and the lambda body respectively. Therefore, once we store each component in a constant (note that again, the empty list is used as error value), we define and register in localContext a function with type (SExpr, [SExpr]?, [SExpr]?)->SExpr that as we’ll see momentarily will be invoked by eval() when the evaluator will find it in an expression.
When it will be used, this anonymous function will evaluate the body of the lambda replacing the original variables list with the current parameters and return the result.
To better understand what is happening there, let’s finally take a look at the eval() function:
public enum SExpr{
case Atom(String)
case List([SExpr])
/**
Evaluates this SExpression with the given functions environment
- Parameter environment: A set of named functions or the default environment
- Returns: the resulting SExpression after evaluation
*/
public func eval(with locals: [SExpr]? = nil, for values: [SExpr]? = nil) -> SExpr?{
var node = self
switch node {
case .Atom:
return evaluateVariable(node, with:locals, for:values)
case var .List(elements):
var skip = false
if elements.count > 1, case let .Atom(value) = elements[0] {
skip = Builtins.mustSkip(value)
}
// Evaluate all subexpressions
if !skip {
elements = elements.map{
return $0.eval(with:locals, for:values)!
}
}
node = .List(elements)
// Obtain a a reference to the function represented by the first atom and apply it, local definitions shadow global ones
if elements.count > 0, case let .Atom(value) = elements[0], let f = localContext[value] ?? defaultEnvironment[value] {
let r = f(node,locals,values)
return r
}
return node
}
}
private func evaluateVariable(_ v: SExpr, with locals: [SExpr]?, for values: [SExpr]?) -> SExpr {
guard let locals = locals, let values = values else {return v}
if locals.contains(v) {
// The current atom is a variable, replace it with its value
return values[locals.index(of: v)!]
}else{
// Not a variable, just return it
return v
}
}
}The evaluator traverses the AST performing different operations depending on the type of the current form is evaluating.
When an atom is encountered, it tries to resolve it as a variable with the current context of local variables (set initially by defun or lambda and propagated between calls) but most of the times it will just return the atom as it is.
This is where the variables substitution for user-defined lambda is performed, we simply verify for each atom if its name is present in the array of the variables and if it is, we replace the atom with the one with the same index from the values array.
We have more to consider when evaluating a list or compound form.
We’ll first try to evaluate recursively all the sub-expressions in the current list, but only if the current operator does not need to handle this evaluation itself. As said above in this simple LISP only quote, special forms and lambda definition operator fall in this category.
Once the sub-expressions have been evaluated, it’s time to apply the operator to its operands and to do this we’ll perform a lookup for a lambda with the same name of the operator atom in localContext and then in defaultEnvironment. The order is important, since we want to be able to shadow the default definitions with new functions we would want to define manually.
If a lambda with that name exists, the function is invoked and the result returned to the previous step of the recursive evaluation.
This concludes the description of the basic interpreter, the whole thing needs more or less 400 lines of code.
SwiftyLisp REPL
It’s time to implement the REPL, but it won’t take long, the interpreter has all the basic functionalities we need.
We’ll read a line from the terminal, convert it to a SExpr, evaluate it and print the result, that will be well formatted thanks to the CustomStringConvertible protocol.
import SwiftyLisp
var exit = false
while(!exit){
print(">>>", terminator:" ")
let input = readLine(strippingNewline: true)
exit = (input=="exit") ? true : false
if !exit {
let e = SExpr.read(input!)
print(e.eval()!)
}
}Conclusion
This article described a minimal LISP interpreter to show you the basic building blocks of interpreters in general regardless of the language.
If you never built something like this before it could seem daunting at first but I hope to have shown that it is definitely something that with a bit of work everyone can do.
Check out the complete project on Github and let me know in the comments if you’d like to read more about interpreters and compilers!