Combing through The Art Of Computer Programming (TAOCP) by Donald Knuth, I’ve found something interesting. Right at the beginning of the book, where he’s stating the basis of his presentation of algorithms, he proposes a different notation for expressing algorithms, that seems to be used only there on section 1.1, and then forgotten for the rest of the book.
Here’s the notation I’m talking about, where Knuth presents the Greatest Common Divisor algorithm.
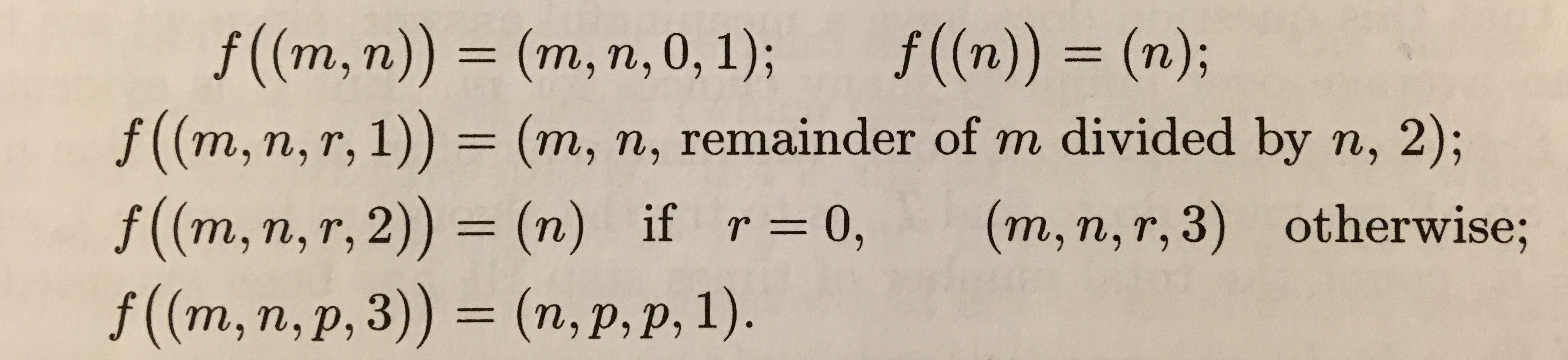
Which to me looks too similar to Erlang’s Syntax. Uses semi-colons ;
to separate function clauses. Function bodies to be executed are
selected by pattern matching its arguments. The last function clause
ends with a period .. It has a guards in the form of if r=0
execute this, otherwise that; and so on.
Let’s translate it to erlang:
-module(algorithm_e).-export([f/1]).f({M,N})->f({M,N,0,1});f({N})->{N};f({M,N,R,1})->f({M,N,MremN,2});f({M,N,R,2})whenR=:=0->f({N});f({M,N,R,2})->f({M,N,R,3});f({M,N,P,3})->f({N,P,P,1}).What we did was to write the variable names in uppercase, since that’s
required in Erlang; we delimited tuples using {} instead of () as
expected in erlang; and finally we wrote guards using the when
keyword. Also instead of assigning function bodies with the equal sign
(=) we used the arrow: ->.
Interesting curiosity, which proves that the Erlang Syntax is some sort of Platonic Language Ideal that predates all programming languages. Now it’s time for Joe and Robert to confess where they got their inspiration from.