This article presents some of the mathematics of Civilization V. It was originally published by alpaca at the CivFanatics forum. Notice that this article represents the state of the game before the December 2010 patch!
Updated on 6/13/2015: Unit Maintenance updated to reflect the actual formula in the DLL - monju125
Calculating Culture![]() Edit
Edit
Border growth![]() Edit
Edit
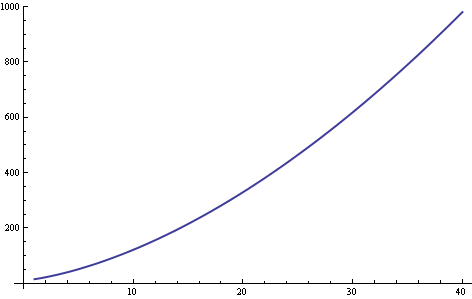
The cost of a border growth is, with t the number of tiles already claimed

Formula for Social Policies![]() Edit
Edit
The first thing we need to know when talking about anything culture-wise is how to calculate it. From the game core XML files and in-game observations, it works like this: You calculate a base cost that depends on the number of policies, then multiply with a factor that depends on your number of cities. As follows:
 : The base cost of policy k. Depends only on the number of policies
: The base cost of policy k. Depends only on the number of policies
 : The number of cities in your empire
: The number of cities in your empire
 : The cost factor depending on the number of cities in your empire
: The cost factor depending on the number of cities in your empire
 : The total cost of policy k. Depends on your number of cities and policies already unlocked
: The total cost of policy k. Depends on your number of cities and policies already unlocked
The policy cost has to be modified depending on your difficulty setting, game speed and map size. I took the numbers from a post by Yamian. Let
 : The map size modifier (0.3 for normal size and below, 0.2 for large, 0.15 for huge)
: The map size modifier (0.3 for normal size and below, 0.2 for large, 0.15 for huge)
 : The map difficulty coefficient (0.5 for settler, 0.67 for chieftain, 0.85 for warlord, 1 otherwise)
: The map difficulty coefficient (0.5 for settler, 0.67 for chieftain, 0.85 for warlord, 1 otherwise)
 : The game speed modifier (3 for marathon, 1.5 for epic, 1 for normal and 0.67 for quick)
: The game speed modifier (3 for marathon, 1.5 for epic, 1 for normal and 0.67 for quick)


The policy cost scales linearly with the number of cities and something between linear and quadratic with the number of policies.
 rounded to the next multiple of 5
rounded to the next multiple of 5
| k=0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| n=1 | 25 | 45 | 90 | 160 | 245 | 345 | 465 | 595 | 745 | 905 | 1075 | 1260 | 1460 | 1670 | 1890 | 2120 | 2365 | 2620 | 2885 | 3160 | 3445 | 3745 | 4050 | 4365 | 4690 | 5025 | 5370 | 5725 | 6090 | 6465 | 6845 |
| 2 | 30 | 55 | 120 | 205 | 320 | 450 | 605 | 775 | 970 | 1175 | 1400 | 1640 | 1900 | 2170 | 2460 | 2760 | 3075 | 3405 | 3750 | 4110 | 4480 | 4865 | 5265 | 5675 | 6100 | 6535 | 6985 | 7445 | 7920 | 8405 | 8900 |
| 3 | 40 | 70 | 145 | 255 | 395 | 555 | 745 | 955 | 1190 | 1445 | 1725 | 2020 | 2335 | 2670 | 3025 | 3395 | 3785 | 4195 | 4620 | 5060 | 5515 | 5990 | 6480 | 6985 | 7510 | 8045 | 8595 | 9165 | 9745 | 10345 | 10955 |
| 4 | 45 | 85 | 175 | 305 | 465 | 660 | 885 | 1135 | 1415 | 1720 | 2050 | 2400 | 2775 | 3175 | 3595 | 4035 | 4500 | 4980 | 5485 | 6010 | 6550 | 7115 | 7695 | 8295 | 8915 | 9555 | 10210 | 10885 | 11575 | 12280 | 13010 |
| 5 | 55 | 100 | 205 | 350 | 540 | 765 | 1025 | 1315 | 1640 | 1990 | 2370 | 2780 | 3215 | 3675 | 4160 | 4670 | 5210 | 5770 | 6350 | 6955 | 7585 | 8240 | 8910 | 9605 | 10325 | 11060 | 11820 | 12600 | 13400 | 14220 | 15065 |
| 6 | 60 | 115 | 230 | 400 | 615 | 870 | 1165 | 1495 | 1865 | 2265 | 2695 | 3160 | 3655 | 4175 | 4730 | 5310 | 5920 | 6555 | 7215 | 7905 | 8620 | 9360 | 10125 | 10920 | 11730 | 12570 | 13435 | 14320 | 15230 | 16160 | 17115 |
| 7 | 70 | 125 | 260 | 450 | 690 | 975 | 1305 | 1675 | 2085 | 2535 | 3020 | 3540 | 4090 | 4680 | 5295 | 5945 | 6630 | 7340 | 8085 | 8855 | 9655 | 10485 | 11345 | 12230 | 13140 | 14080 | 15045 | 16040 | 17055 | 18100 | 19170 |
| 8 | 75 | 140 | 285 | 495 | 765 | 1080 | 1445 | 1855 | 2310 | 2805 | 3345 | 3915 | 4530 | 5180 | 5865 | 6585 | 7340 | 8130 | 8950 | 9805 | 10690 | 11610 | 12560 | 13540 | 14550 | 15590 | 16660 | 17755 | 18885 | 20040 | 21225 |
| 9 | 85 | 155 | 315 | 545 | 835 | 1185 | 1585 | 2035 | 2535 | 3080 | 3665 | 4295 | 4970 | 5680 | 6430 | 7220 | 8050 | 8915 | 9815 | 10755 | 11725 | 12735 | 13775 | 14850 | 15955 | 17100 | 18270 | 19475 | 20715 | 21980 | 23280 |
| 10 | 90 | 170 | 345 | 595 | 910 | 1290 | 1725 | 2215 | 2760 | 3350 | 3990 | 4675 | 5405 | 6180 | 7000 | 7860 | 8760 | 9700 | 10685 | 11705 | 12760 | 13855 | 14990 | 16160 | 17365 | 18605 | 19885 | 21195 | 22540 | 23920 | 25335 |
| 11 | 100 | 180 | 370 | 640 | 985 | 1395 | 1865 | 2395 | 2985 | 3620 | 4315 | 5055 | 5845 | 6685 | 7570 | 8495 | 9470 | 10490 | 11550 | 12650 | 13795 | 14980 | 16205 | 17470 | 18775 | 20115 | 21495 | 22915 | 24370 | 25860 | 27390 |
| 12 | 105 | 195 | 400 | 690 | 1060 | 1500 | 2005 | 2575 | 3205 | 3895 | 4635 | 5435 | 6285 | 7185 | 8135 | 9135 | 10180 | 11275 | 12415 | 13600 | 14830 | 16105 | 17420 | 18780 | 20180 | 21625 | 23110 | 24630 | 26195 | 27800 | 29445 |
| 13 | 115 | 210 | 425 | 740 | 1135 | 1605 | 2145 | 2755 | 3430 | 4165 | 4960 | 5815 | 6725 | 7685 | 8705 | 9770 | 10895 | 12065 | 13280 | 14550 | 15865 | 17230 | 18635 | 20090 | 21590 | 23135 | 24720 | 26350 | 28025 | 29740 | 31495 |
| 14 | 120 | 225 | 455 | 785 | 1210 | 1710 | 2285 | 2935 | 3655 | 4440 | 5285 | 6195 | 7160 | 8190 | 9270 | 10410 | 11605 | 12850 | 14150 | 15500 | 16900 | 18350 | 19850 | 21400 | 23000 | 24640 | 26330 | 28070 | 29850 | 31680 | 33550 |
| 15 | 130 | 235 | 485 | 835 | 1280 | 1815 | 2425 | 3115 | 3880 | 4710 | 5610 | 6575 | 7600 | 8690 | 9840 | 11045 | 12315 | 13635 | 15015 | 16450 | 17935 | 19475 | 21070 | 22710 | 24405 | 26150 | 27945 | 29790 | 31680 | 33620 | 35605 |
| 16 | 135 | 250 | 510 | 885 | 1355 | 1920 | 2570 | 3295 | 4100 | 4980 | 5930 | 6950 | 8040 | 9190 | 10405 | 11685 | 13025 | 14425 | 15880 | 17395 | 18970 | 20600 | 22285 | 24020 | 25815 | 27660 | 29555 | 31505 | 33505 | 35560 | 37660 |
| 17 | 145 | 265 | 540 | 930 | 1430 | 2025 | 2710 | 3475 | 4325 | 5255 | 6255 | 7330 | 8475 | 9690 | 10975 | 12320 | 13735 | 15210 | 16750 | 18345 | 20005 | 21725 | 23500 | 25330 | 27220 | 29170 | 31170 | 33225 | 35335 | 37500 | 39715 |
| 18 | 150 | 280 | 565 | 980 | 1505 | 2130 | 2850 | 3655 | 4550 | 5525 | 6580 | 7710 | 8915 | 10195 | 11540 | 12960 | 14445 | 15995 | 17615 | 19295 | 21040 | 22845 | 24715 | 26645 | 28630 | 30675 | 32780 | 34945 | 37165 | 39440 | 41770 |
| 19 | 160 | 290 | 595 | 1030 | 1580 | 2235 | 2990 | 3835 | 4775 | 5795 | 6905 | 8090 | 9355 | 10695 | 12110 | 13595 | 15155 | 16785 | 18480 | 20245 | 22075 | 23970 | 25930 | 27955 | 30040 | 32185 | 34395 | 36665 | 38990 | 41380 | 43825 |
| 20 | 165 | 305 | 625 | 1075 | 1650 | 2340 | 3130 | 4015 | 5000 | 6070 | 7225 | 8470 | 9795 | 11195 | 12680 | 14235 | 15865 | 17570 | 19345 | 21195 | 23110 | 25095 | 27145 | 29265 | 31445 | 33695 | 36005 | 38380 | 40820 | 43320 | 45880 |
| 21 | 175 | 320 | 650 | 1125 | 1725 | 2445 | 3270 | 4195 | 5220 | 6340 | 7550 | 8850 | 10230 | 11700 | 13245 | 14870 | 16575 | 18360 | 20215 | 22145 | 24145 | 26220 | 28360 | 30575 | 32855 | 35205 | 37620 | 40100 | 42645 | 45255 | 47930 |
| 22 | 180 | 335 | 680 | 1175 | 1800 | 2550 | 3410 | 4375 | 5445 | 6615 | 7875 | 9230 | 10670 | 12200 | 13815 | 15510 | 17285 | 19145 | 21080 | 23090 | 25180 | 27340 | 29575 | 31885 | 34265 | 36710 | 39230 | 41820 | 44475 | 47195 | 49985 |
| 23 | 190 | 345 | 705 | 1220 | 1875 | 2655 | 3550 | 4555 | 5670 | 6885 | 8200 | 9605 | 11110 | 12700 | 14380 | 16145 | 18000 | 19930 | 21945 | 24040 | 26215 | 28465 | 30790 | 33195 | 35670 | 38220 | 40845 | 43540 | 46300 | 49135 | 52040 |
| 24 | 195 | 360 | 735 | 1270 | 1950 | 2760 | 3690 | 4735 | 5895 | 7155 | 8520 | 9985 | 11550 | 13200 | 14950 | 16785 | 18710 | 20720 | 22815 | 24990 | 27250 | 29590 | 32010 | 34505 | 37080 | 39730 | 42455 | 45255 | 48130 | 51075 | 54095 |
| 25 | 205 | 375 | 765 | 1320 | 2025 | 2865 | 3830 | 4915 | 6115 | 7430 | 8845 | 10365 | 11985 | 13705 | 15515 | 17420 | 19420 | 21505 | 23680 | 25940 | 28285 | 30715 | 33225 | 35815 | 38490 | 41240 | 44070 | 46975 | 49960 | 53015 | 56150 |
| 26 | 210 | 390 | 790 | 1365 | 2095 | 2970 | 3970 | 5095 | 6340 | 7700 | 9170 | 10745 | 12425 | 14205 | 16085 | 18060 | 20130 | 22290 | 24545 | 26890 | 29320 | 31835 | 34440 | 37125 | 39895 | 42750 | 45680 | 48695 | 51785 | 54955 | 58205 |
| 27 | 220 | 405 | 820 | 1415 | 2170 | 3070 | 4110 | 5275 | 6565 | 7970 | 9495 | 11125 | 12865 | 14705 | 16650 | 18695 | 20840 | 23080 | 25410 | 27835 | 30355 | 32960 | 35655 | 38435 | 41305 | 44255 | 47295 | 50410 | 53615 | 56895 | 60260 |
| 28 | 225 | 415 | 845 | 1465 | 2245 | 3175 | 4250 | 5455 | 6790 | 8245 | 9815 | 11505 | 13300 | 15210 | 17220 | 19335 | 21550 | 23865 | 26280 | 28785 | 31390 | 34085 | 36870 | 39745 | 42710 | 45765 | 48905 | 52130 | 55440 | 58835 | 62315 |
| 29 | 235 | 430 | 875 | 1510 | 2320 | 3280 | 4390 | 5635 | 7015 | 8515 | 10140 | 11885 | 13740 | 15710 | 17790 | 19970 | 22260 | 24655 | 27145 | 29735 | 32425 | 35210 | 38085 | 41055 | 44120 | 47275 | 50520 | 53850 | 57270 | 60775 | 64365 |
| 30 | 240 | 445 | 905 | 1560 | 2395 | 3385 | 4530 | 5815 | 7235 | 8790 | 10465 | 12265 | 14180 | 16210 | 18355 | 20610 | 22970 | 25440 | 28010 | 30685 | 33460 | 36330 | 39300 | 42370 | 45530 | 48785 | 52130 | 55570 | 59095 | 62715 | 66420 |
| 31 | 250 | 460 | 930 | 1610 | 2470 | 3490 | 4670 | 5995 | 7460 | 9060 | 10790 | 12640 | 14620 | 16710 | 18925 | 21245 | 23680 | 26225 | 28875 | 31635 | 34495 | 37455 | 40515 | 43680 | 46935 | 50290 | 53740 | 57285 | 60925 | 64655 | 68475 |
| 32 | 255 | 470 | 960 | 1655 | 2540 | 3595 | 4810 | 6175 | 7685 | 9330 | 11110 | 13020 | 15055 | 17215 | 19490 | 21885 | 24395 | 27015 | 29745 | 32585 | 35530 | 38580 | 41735 | 44990 | 48345 | 51800 | 55355 | 59005 | 62755 | 66595 | 70530 |
| 33 | 265 | 485 | 985 | 1705 | 2615 | 3700 | 4950 | 6355 | 7910 | 9605 | 11435 | 13400 | 15495 | 17715 | 20060 | 22520 | 25105 | 27800 | 30610 | 33530 | 36565 | 39700 | 42950 | 46300 | 49755 | 53310 | 56965 | 60725 | 64580 | 68535 | 72585 |
| 34 | 270 | 500 | 1015 | 1755 | 2690 | 3805 | 5090 | 6535 | 8130 | 9875 | 11760 | 13780 | 15935 | 18215 | 20625 | 23160 | 25815 | 28585 | 31475 | 34480 | 37600 | 40825 | 44165 | 47610 | 51160 | 54820 | 58580 | 62445 | 66410 | 70475 | 74640 |
| 35 | 280 | 515 | 1045 | 1800 | 2765 | 3910 | 5230 | 6715 | 8355 | 10145 | 12085 | 14160 | 16370 | 18720 | 21195 | 23795 | 26525 | 29375 | 32345 | 35430 | 38635 | 41950 | 45380 | 48920 | 52570 | 56325 | 60190 | 64160 | 68235 | 72415 | 76695 |
| 36 | 285 | 525 | 1070 | 1850 | 2840 | 4015 | 5370 | 6895 | 8580 | 10420 | 12405 | 14540 | 16810 | 19220 | 21760 | 24435 | 27235 | 30160 | 33210 | 36380 | 39670 | 43075 | 46595 | 50230 | 53980 | 57835 | 61805 | 65880 | 70065 | 74355 | 78745 |
| 37 | 295 | 540 | 1100 | 1900 | 2910 | 4120 | 5510 | 7075 | 8805 | 10690 | 12730 | 14920 | 17250 | 19720 | 22330 | 25070 | 27945 | 30950 | 34075 | 37330 | 40705 | 44195 | 47810 | 51540 | 55385 | 59345 | 63415 | 67600 | 71890 | 76295 | 80800 |
| 38 | 300 | 555 | 1125 | 1945 | 2985 | 4225 | 5650 | 7255 | 9030 | 10960 | 13055 | 15295 | 17690 | 20225 | 22895 | 25710 | 28655 | 31735 | 34940 | 38275 | 41735 | 45320 | 49025 | 52850 | 56795 | 60855 | 65030 | 69320 | 73720 | 78235 | 82855 |
| 39 | 310 | 570 | 1155 | 1995 | 3060 | 4330 | 5790 | 7435 | 9250 | 11235 | 13380 | 15675 | 18125 | 20725 | 23465 | 26345 | 29365 | 32520 | 35810 | 39225 | 42770 | 46445 | 50240 | 54160 | 58200 | 62365 | 66640 | 71035 | 75545 | 80170 | 84910 |
| 40 | 315 | 580 | 1185 | 2045 | 3135 | 4435 | 5930 | 7615 | 9475 | 11505 | 13700 | 16055 | 18565 | 21225 | 24035 | 26985 | 30075 | 33310 | 36675 | 40175 | 43805 | 47570 | 51455 | 55470 | 59610 | 63870 | 68255 | 72755 | 77375 | 82110 | 86965 |
| 41 | 325 | 595 | 1210 | 2090 | 3210 | 4540 | 6070 | 7795 | 9700 | 11780 | 14025 | 16435 | 19005 | 21725 | 24600 | 27620 | 30790 | 34095 | 37540 | 41125 | 44840 | 48690 | 52675 | 56780 | 61020 | 65380 | 69865 | 74475 | 79205 | 84050 | 89020 |
| 42 | 330 | 610 | 1240 | 2140 | 3285 | 4645 | 6215 | 7975 | 9925 | 12050 | 14350 | 16815 | 19440 | 22230 | 25170 | 28260 | 31500 | 34880 | 38410 | 42075 | 45875 | 49815 | 53890 | 58095 | 62425 | 66890 | 71480 | 76195 | 81030 | 85990 | 91075 |
| 43 | 340 | 625 | 1265 | 2190 | 3355 | 4750 | 6355 | 8155 | 10145 | 12320 | 14670 | 17195 | 19880 | 22730 | 25735 | 28895 | 32210 | 35670 | 39275 | 43025 | 46910 | 50940 | 55105 | 59405 | 63835 | 68400 | 73090 | 77910 | 82860 | 87930 | 93130 |
| 44 | 345 | 635 | 1295 | 2235 | 3430 | 4855 | 6495 | 8335 | 10370 | 12595 | 14995 | 17575 | 20320 | 23230 | 26305 | 29535 | 32920 | 36455 | 40140 | 43970 | 47945 | 52065 | 56320 | 60715 | 65245 | 69905 | 74705 | 79630 | 84685 | 89870 | 95180 |
| 45 | 355 | 650 | 1325 | 2285 | 3505 | 4960 | 6635 | 8515 | 10595 | 12865 | 15320 | 17955 | 20760 | 23735 | 26870 | 30170 | 33630 | 37240 | 41005 | 44920 | 48980 | 53185 | 57535 | 62025 | 66650 | 71415 | 76315 | 81350 | 86515 | 91810 | 97235 |
| 46 | 360 | 665 | 1350 | 2335 | 3580 | 5065 | 6775 | 8695 | 10820 | 13135 | 15645 | 18330 | 21195 | 24235 | 27440 | 30810 | 34340 | 38030 | 41875 | 45870 | 50015 | 54310 | 58750 | 63335 | 68060 | 72925 | 77930 | 83065 | 88340 | 93750 | 99290 |
| 47 | 370 | 680 | 1380 | 2380 | 3655 | 5170 | 6915 | 8875 | 11045 | 13410 | 15965 | 18710 | 21635 | 24735 | 28005 | 31445 | 35050 | 38815 | 42740 | 46820 | 51050 | 55435 | 59965 | 64645 | 69465 | 74435 | 79540 | 84785 | 90170 | 95690 | 101345 |
| 48 | 375 | 695 | 1405 | 2430 | 3725 | 5275 | 7055 | 9055 | 11265 | 13680 | 16290 | 19090 | 22075 | 25235 | 28575 | 32085 | 35760 | 39605 | 43605 | 47770 | 52085 | 56560 | 61180 | 65955 | 70875 | 75940 | 81150 | 86505 | 92000 | 97630 | 103400 |
| 49 | 385 | 705 | 1435 | 2480 | 3800 | 5380 | 7195 | 9235 | 11490 | 13955 | 16615 | 19470 | 22515 | 25740 | 29145 | 32720 | 36470 | 40390 | 44475 | 48715 | 53120 | 57680 | 62395 | 67265 | 72285 | 77450 | 82765 | 88225 | 93825 | 99570 | 105455 |
| 50 | 390 | 720 | 1465 | 2525 | 3875 | 5485 | 7335 | 9415 | 11715 | 14225 | 16940 | 19850 | 22950 | 26240 | 29710 | 33360 | 37185 | 41175 | 45340 | 49665 | 54155 | 58805 | 63615 | 68575 | 73690 | 78960 | 84375 | 89940 | 95655 | 101510 | 107510 |
How fast do I acquire new policies?![]() Edit
Edit
This is very simple, and I'll just list it here to introduce some variable names. It depends on the culture your empire yields. With
 : The total culture yield of your empire
: The total culture yield of your empire
 : The cost of your next social policy (I will omit the dependencies for readability)
: The cost of your next social policy (I will omit the dependencies for readability)
 : The time in turns to unlock the next policy
: The time in turns to unlock the next policy
we get the simple formula

if we assume we just unlocked a new policy. If we introduce
 : The culture already accumulated in the culture bucket
: The culture already accumulated in the culture bucket
we get

How do I calculate the total culture in my empire?![]() Edit
Edit
This is shown in the UI but again to introduce some concepts. Let
 : the average culture of each city in your empire
: the average culture of each city in your empire
It makes sense to split c up into a part that depends on n and represents your "typical city culture", the culture each city you newly create will add to your empire, and a part that is constant in n and represents bonuses from wonders, landmarks and city states. This is exact if you immediately buy your typical culture buildings but normally it's an approximation (it represents an equilibrium you will not normally have reached)
 : The typical culture per city
: The typical culture per city
 : The city state culture
: The city state culture

Before I continue let's look at the policy speed for large numbers


Also:
So for large n, the average amount of culture per city is a good measure for the policy speed.
Will expanding increase or decrease policy speed?![]() Edit
Edit
This is the question Paeanblack and I discussed in said thread. To analyse this, we have to calculate the number of turns to the next policy and see how it's affected by going from n->n+1.
When we do the city number increase, both p and c change. Let p and c be the policy cost and culture yield before founding the new city and p' and c' be the respective numbers after the founding.


Then calculate t' and check when it gets smaller than t (this would signify an increased policy speed)





For standard-sized maps,  so
so

So if the base culture from city states is less than 7/3 times larger than the typical city culture (let's call this the culture ratio r_c), you will get an increased policy speed from expanding. If it's exactly equal to this, the speed will stay the same, and if it's more, policy speed will slow. It should be noted that, no matter the value of r_c, for large numbers of cities the increase or decrease for founding an additional city will be very small.
For larger maps, this will be a little different.
- Large: r_c < 4
- Huge: r_c < 17/3 =5.\hat6
Numbers![]() Edit
Edit
Now we can plug in some example numbers into our calculations. I will discuss the results only for the standard map size
- Let's assume you only build a monument in each of your cities. This is equivalent to a value of cT = 2. So if cC is five or greater, for example because you have at least one cultural city state as a friend, expansion will slow down your social policy speed.
Standard: cC > 4, Large: cC > 8, Huge: cC > 11 - Now assume we build a monument and a temple, or cT = 5. Then, cC <= 11 will still yield an increase in your social policy speed. A cC of 10 is still pretty low, though. You normally still get it later on if you have at least one cultural city state ally.
Standard: cC > 11, Large: cC > 20, Huge: cC > 28 - Looking at France, with a monument cT = 4 (true also for Egypt with Monument and Burial Tomb) and with both monument and temple, cT = 7. The corresponding cC values are 9 and 16. For 9 the same as above is true, but for the case with temples, you will actually gain an increase in policy speed if you don't have at least two city state allies or a city state and a few wonders.
Standard: cC > 9 or 16, Large: cC > 16 or 28, Huge: cC > 28 or 40 - The Songhai have the excellent Mud Pyramid, so they share the cT = 7 case with France. The same goes for adding two artists in each city.
To sum up, expanding will in almost all cases slow down your social progress. The only cases where it will speed it up are if you either aren't interested in city states and wonders, or if you play a civ with a culture bonus. The only somewhat realistic scenario where expansion could speed up your policy gain is in my opinion if you play Songhai because you'll really want the Mud Pyramid and a Monument isn't that expensive.
I'm not sure if city state bonuses scale with the map size but if they don't, expansion increasing your policy speed is a lot more likely on larger maps, probably happening at some time if you just have a monument and a temple or are playing France. If you play Songhai, or France with temples it will even happen pretty often in fact. This is another case where the game doesn't scale well (well in the sense of preserving the same effects on gameplay as on standard size) with map size.
Food cost![]() Edit
Edit
The food cost for a city to grow is calculated as follows
 : The number of citizens in the city
: The number of citizens in the city
 : Amount of food to grow to size n+1
: Amount of food to grow to size n+1
 rounded down to the next integer.
rounded down to the next integer.
Here are some tabularized and plotted values:
- Food required to grow to level n+1
Code:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | 15 | 22 | 30 | 40 | 51 | 63 | 76 | 90 | 105 | 121 | 138 | 155 | 174 | 194 | 214 | 235 | 258 | 280 | 304 | 329 | 354 | 380 | 407 | 435 | 464 | 493 | 523 | 554 | 585 | 617 | 650 | 684 | 719 | 754 | 790 | 826 | 863 | 901 | 940 | 979 |
- Integrated food values (total amount food it takes to grow to size n)
Code:
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | 15 | 37 | 67 | 107 | 158 | 221 | 297 | 387 | 492 | 613 | 751 | 906 | 1080 | 1274 | 1488 | 1723 | 1981 | 2261 | 2565 | 2894 | 3248 | 3628 | 4035 | 4470 | 4934 | 5427 | 5950 | 6504 | 7089 | 7706 | 8356 | 9040 | 9759 | 10513 | 11303 | 12129 | 12992 | 13893 | 14833 | 15812 |
What this means is that growing from size 5 to 6 costs 51 food, while growing from size 10 to 11 already costs 122 food. I would like to present a few ways of looking at this problem from different angles in the following.
Constant Food Surplus![]() Edit
Edit
This simplification assumes that each new citizen will work a tile that's worth 2 food and you therefore have a constant amount of food surplus that is put into growth. For a normal city without any bonuses, the amount of turns you need to grow is simply given by

where n is the number of citizens, f the food surplus and t the number of turns until growth, assuming you start at 0 food. Let's look at the numbers for df = 8
Code:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t | 2 | 3 | 4 | 5 | 6 | 8 | 10 | 11 | 13 | 15 | 17 | 19 | 22 | 24 | 27 | 29 | 32 | 35 | 38 | 41 | 44 | 48 | 51 | 54 | 58 | 62 | 65 | 69 | 73 | 77 | 81 | 86 | 90 | 94 | 99 | 103 | 108 | 113 | 118 | 122 |
This kind of explains why growth feels so slow once you hit the teens: The number of turns cities need to grow becomes pretty large, even with a pretty decent food surplus. A city takes about the same time to grow from size 12 to 13 as from size 1 to 5.
Constant food per citizen![]() Edit
Edit
Here, the assumption is that each citizen will yield a certain mean amount of food. To understand what happens there better, let's define another function, the average growth cost per citizen

(In blue the exact function, in red the rounded one the game uses)
The last term is approximately n^0.8 and dominates for large n. As you can see, this function has a minimum at size 4 (about 3.75 in the continuous case) and then constantly grows a little less than linearly - but linear growth is an excellent approximation.
As you can see below, the function 0.41 n + 8.18 fits the data over this range perfectly but is much simpler (the functions agree at all integer places).
So how do you interpret this function? What it tells you is that, with a constant amount of food produced per citizen, your city will grow more quickly than before until it hits size 4, and then starts slowing down again. Or, to put it more simple, this function tells you the amount of food each citizen has to produce to let the city grow.
An alternative, but equivalent, point of view is that, if you're aiming for a constant city growth speed, each citizen has to become more efficient as your city grows, in an approximately linear function.
You should note that the amount of food generated per citizen will usually be larger for small cities due to the city square itself (especially with maritime CS).
Slightly more realistic![]() Edit
Edit
Cities start with a center square that yields some food (this catches granary, maritime city-states and water mill food, too). So the assumption that the amount of food per citizen will stay the same isn't really completely applicable. So let's introduce a new variable, f_csq, the city square food amount.
The assumption of an average amount of food per citizen now makes sense if you leave the city square food out. So let's call the amount of food each citizen generates f_c. The total food per turn, f, is then given by

More interesting for us is the food surplus. This is given by

The amount of surplus food produced per citizen is then

To get the number of turns we need for growth, we need to combine this with the food growth cost and get

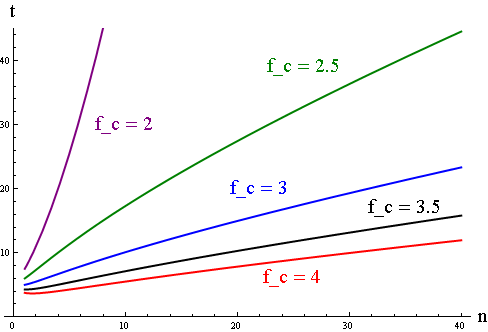
Since this function doesn't read too pretty, I'll just plop in some numbers and give you a graphical representation. Let's say f_csq = 2, which is the case if you don't have city state allies. If the city is to grow in a reasonable amount of time, f_c should be greater than 2.5, as you can see below
You will notice a local minimum evolving in the f_c = 4 case, which signifies the onset of the constant food per citizen approximation, which is the limiting case for f_csq = 0
Are granaries worth it?![]() Edit
Edit
Ultimately, that's for you to decide. I can give you some information so you can make an educated decision, though. Granaries increase f_csq from 2 to 4, so let's look at what happens to t if we make that change. Dashed are the values without granary, the full lines are with a granary
More useful to judge the granary's effects is looking at the difference between the case without a granary, and the case with a granary
As you can see, the difference quickly becomes essentially constant at a city size of 10 or more for any case of f_c > 2. From this analysis, I'd say that for f_c values up to 3, a granary is generally worth it, because it saves you a turn or two per growth step. For f_c = 2.5 it's very much worth it, and this seems to be a more realistic case than the higher values because not every citizen will work a farm (the f_c = 4 case represents each citizen working a Civil Service/Fertilizer farm) and some won't produce any food at all, like specialists.
Other f_csq effects![]() Edit
Edit
We can continue this analysis by increasing f_csq in steps. For example, a maritime CS will yield 2 extra food, as will a water wheel. Let's see what happens if we go from f_csq = 4 to f_csq = 6. I will omit the more unrealistically high cases from now on for a better overview. Shown is again the total number of turns needed and the difference between 4 and 6. This time, f_csq = 4 is dashed
So getting the second city-state isn't as good as getting the first, and getting a granary when you already have a city-state isn't so great, either. It still shaves off a turn (or three in the f_c = 2.5 case), though.
The next increase step, from 6 to 8 (the "before" being dashed as usual)
Now things start becoming somewhat underwhelming. As I said, if things are worth it for you is up to you to decide, but I'd definitely not build that water mill if I already have a granary and a city-state ally because the difference will only be something like two turns in three growth steps or so, which isn't exactly a lot.
f_c values < 2![]() Edit
Edit
After reading a comment from ehrgeix, I think it makes sense to extend the analysis to f_c values that are smaller than 2. The values greater than 2 are applicable if you want to let your city continue to grow for the rest of the game. Values smaller than 2 still make sense in transitionary periods, if you want a growth cap, or if you're fine with your growth speed slowing down even more than in the constant food surplus case discussed above.
Qualitatively, we can already see from looking at  , which occurs as the denominator in the formula for t, that these functions will have a pole at a finite n, because f_c - 2 becomes negative. The locus of this singularity is given by
, which occurs as the denominator in the formula for t, that these functions will have a pole at a finite n, because f_c - 2 becomes negative. The locus of this singularity is given by  . This singularity signifies the number of citizens where the city stops growing.
. This singularity signifies the number of citizens where the city stops growing.
In the following are some graphs in the same way as above. First, f_csq = 2
If you increase f_csq you shift the position of the pole to the right, so the difference between t(csq = 2) - t(csq = 4) has a singularity at the same points as t. See the f_csq = 4 case below. Dashed is the "previous", in this case f_csq = 2
f_csq = 4 -> f_csq = 6
f_csq = 6 -> f_csq = 8
Unit maintenance![]() Edit
Edit
As of 6/2015, the formula for unit maintenance as defined in all versions CvGameCoreDLL is calculated as follows:
- b = Base unit cost (INITIAL_GOLD_PER_UNIT_TIMES_100)
- f = Free units from handicap (GoldFreeUnits), specific unit types, or policies
- u = Total paid units
- n = max(0, u-f) = Number of actual paid units (if u-f is less than 0 then n = 0)
- m = Multiplier (UNIT_MAINTENANCE_GAME_MULTIPLIER)
- d = Divisor (UNIT_MAINTENANCE_GAME_EXPONENT_DIVISOR)
- t = Current turn
- e = Estimated end turn (based on all entries for the current GameSpeed in GameSpeed_Turns)
- g = t/e = Game progress factor
final cost = (n*b(1+g*m)/100)(1+(g/d))
Unit cost modifiers from traits are applied before the exponent. Unit cost modifiers from policies, handicap, and AI difficulty level are applied to the final cost.
Since there's no easy "each unit in turn t will cost this much" here's a table you can use as a rough reference. The first row is the number of turns, the first column the number of units
| Turns | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Units | 1 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
| 4 | 2 | 2 | 3 | 5 | 7 | 9 | 11 | 14 | 17 | 20 |
| 8 | 4 | 5 | 7 | 11 | 15 | 19 | 24 | 30 | 36 | 43 |
| 12 | 6 | 8 | 11 | 16 | 23 | 30 | 38 | 47 | 57 | 68 |
| 16 | 8 | 10 | 14 | 22 | 31 | 41 | 52 | 64 | 78 | 94 |
| 20 | 10 | 13 | 18 | 28 | 39 | 52 | 66 | 82 | 100 | 121 |
| 24 | 12 | 16 | 22 | 34 | 47 | 63 | 80 | 100 | 122 | 148 |
| 28 | 14 | 18 | 26 | 40 | 56 | 74 | 94 | 118 | 145 | 176 |
| 32 | 16 | 21 | 30 | 46 | 64 | 85 | 109 | 136 | 168 | 204 |
| 36 | 18 | 24 | 34 | 52 | 73 | 96 | 124 | 155 | 191 | 232 |
| 40 | 20 | 26 | 37 | 58 | 81 | 108 | 138 | 174 | 215 | 261 |
| 44 | 22 | 29 | 41 | 64 | 89 | 119 | 153 | 193 | 238 | 291 |
| 48 | 24 | 32 | 45 | 70 | 98 | 131 | 168 | 212 | 262 | 321 |
| 52 | 26 | 35 | 49 | 76 | 107 | 142 | 184 | 231 | 287 | 350 |
| 56 | 28 | 37 | 53 | 82 | 115 | 154 | 199 | 251 | 311 | 381 |
| 60 | 30 | 40 | 57 | 88 | 124 | 166 | 214 | 270 | 335 | 411 |
| 64 | 32 | 43 | 61 | 94 | 133 | 177 | 229 | 290 | 360 | 442 |
| 68 | 34 | 45 | 64 | 100 | 141 | 189 | 245 | 310 | 385 | 473 |
| 72 | 36 | 48 | 68 | 106 | 150 | 201 | 260 | 330 | 410 | 504 |
| 76 | 38 | 51 | 72 | 112 | 159 | 213 | 276 | 349 | 435 | 535 |
| 80 | 40 | 54 | 76 | 118 | 167 | 225 | 292 | 370 | 461 | 567 |
| 84 | 42 | 56 | 80 | 124 | 176 | 237 | 307 | 390 | 486 | 598 |
| 88 | 44 | 59 | 84 | 130 | 185 | 249 | 323 | 410 | 512 | 630 |
| 92 | 46 | 62 | 88 | 137 | 194 | 260 | 339 | 430 | 537 | 662 |
| 96 | 48 | 64 | 92 | 143 | 203 | 273 | 354 | 451 | 563 | 694 |
| 100 | 50 | 67 | 95 | 149 | 211 | 285 | 370 | 471 | 589 | 727 |
Here's an equivalent table detailing the cost per unit
| Turns | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Units | 1 | 20 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 |
| 4 | 0.50 | 0.50 | 0.75 | 1.3 | 1.8 | 2.3 | 2.8 | 3.5 | 4.3 | 5.0 |
| 8 | 0.50 | 0.63 | 0.88 | 1.4 | 1.9 | 2.4 | 3.0 | 3.8 | 4.5 | 5.4 |
| 12 | 0.50 | 0.67 | 0.92 | 1.3 | 1.9 | 2.5 | 3.2 | 3.9 | 4.8 | 5.7 |
| 16 | 0.50 | 0.63 | 0.88 | 1.4 | 1.9 | 2.6 | 3.3 | 4.0 | 4.9 | 5.9 |
| 20 | 0.50 | 0.65 | 0.90 | 1.4 | 2.0 | 2.6 | 3.3 | 4.1 | 5.0 | 6.1 |
| 24 | 0.50 | 0.67 | 0.92 | 1.4 | 2.0 | 2.6 | 3.3 | 4.2 | 5.1 | 6.2 |
| 28 | 0.50 | 0.64 | 0.93 | 1.4 | 2.0 | 2.6 | 3.4 | 4.2 | 5.2 | 6.3 |
| 32 | 0.50 | 0.66 | 0.94 | 1.4 | 2.0 | 2.7 | 3.4 | 4.3 | 5.3 | 6.4 |
| 36 | 0.50 | 0.67 | 0.94 | 1.4 | 2.0 | 2.7 | 3.4 | 4.3 | 5.3 | 6.4 |
| 40 | 0.50 | 0.65 | 0.93 | 1.5 | 2.0 | 2.7 | 3.5 | 4.4 | 5.4 | 6.5 |
| 44 | 0.50 | 0.66 | 0.93 | 1.5 | 2.0 | 2.7 | 3.5 | 4.4 | 5.4 | 6.6 |
| 48 | 0.50 | 0.67 | 0.94 | 1.5 | 2.0 | 2.7 | 3.5 | 4.4 | 5.5 | 6.7 |
| 52 | 0.50 | 0.67 | 0.94 | 1.5 | 2.1 | 2.7 | 3.5 | 4.4 | 5.5 | 6.7 |
| 56 | 0.50 | 0.66 | 0.95 | 1.5 | 2.1 | 2.8 | 3.6 | 4.5 | 5.6 | 6.8 |
| 60 | 0.50 | 0.67 | 0.95 | 1.5 | 2.1 | 2.8 | 3.6 | 4.5 | 5.6 | 6.9 |
| 64 | 0.50 | 0.67 | 0.95 | 1.5 | 2.1 | 2.8 | 3.6 | 4.5 | 5.6 | 6.9 |
| 68 | 0.50 | 0.66 | 0.94 | 1.5 | 2.1 | 2.8 | 3.6 | 4.6 | 5.7 | 7.0 |
| 72 | 0.50 | 0.67 | 0.94 | 1.5 | 2.1 | 2.8 | 3.6 | 4.6 | 5.7 | 7.0 |
| 76 | 0.50 | 0.67 | 0.95 | 1.5 | 2.1 | 2.8 | 3.6 | 4.6 | 5.7 | 7.0 |
| 80 | 0.50 | 0.68 | 0.95 | 1.5 | 2.1 | 2.8 | 3.7 | 4.6 | 5.8 | 7.1 |
| 84 | 0.50 | 0.67 | 0.95 | 1.5 | 2.1 | 2.8 | 3.7 | 4.6 | 5.8 | 7.1 |
| 88 | 0.50 | 0.67 | 0.95 | 1.5 | 2.1 | 2.8 | 3.7 | 4.7 | 5.8 | 7.2 |
| 92 | 0.50 | 0.67 | 0.96 | 1.5 | 2.1 | 2.8 | 3.7 | 4.7 | 5.8 | 7.2 |
| 96 | 0.50 | 0.67 | 0.96 | 1.5 | 2.1 | 2.8 | 3.7 | 4.7 | 5.9 | 7.2 |
| 100 | 0.50 | 0.67 | 0.95 | 1.5 | 2.1 | 2.9 | 3.7 | 4.7 | 5.9 | 7.3 |